Geometry

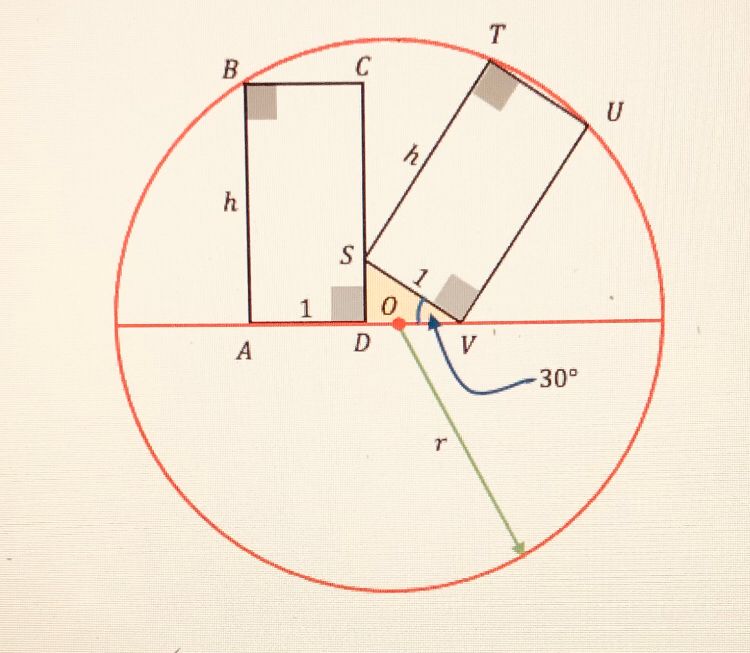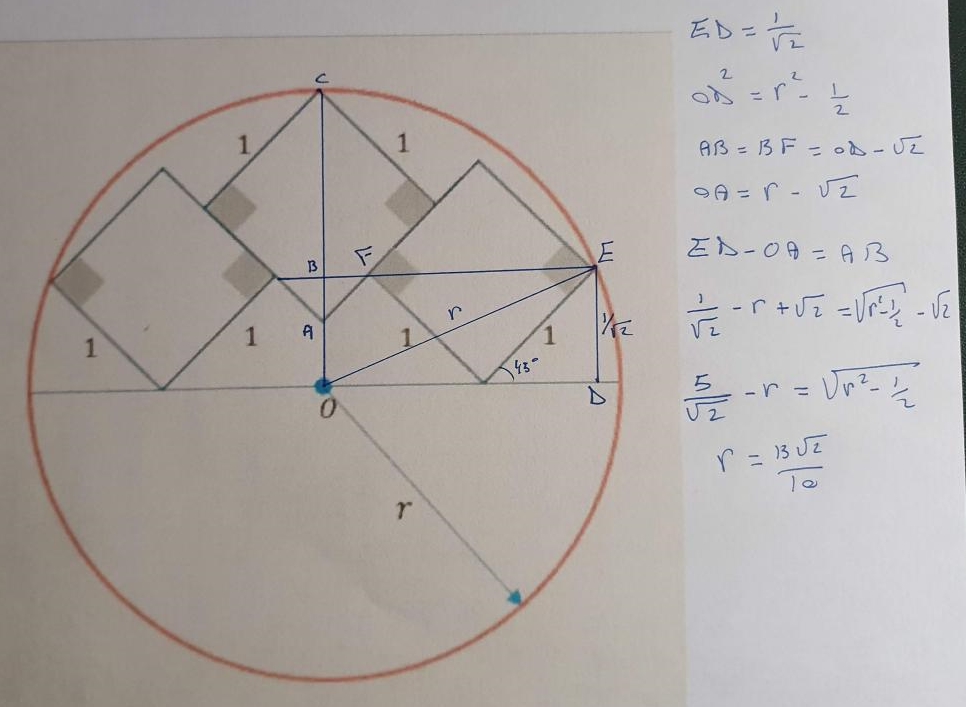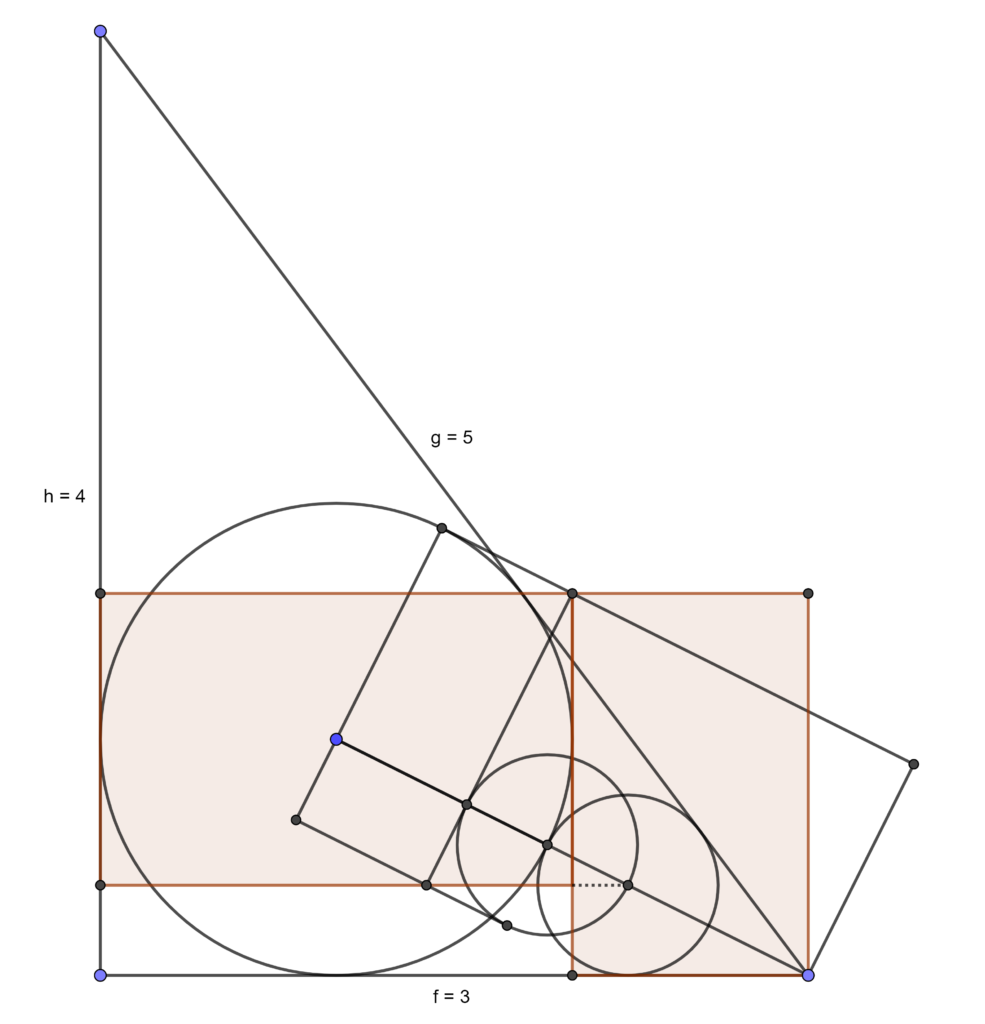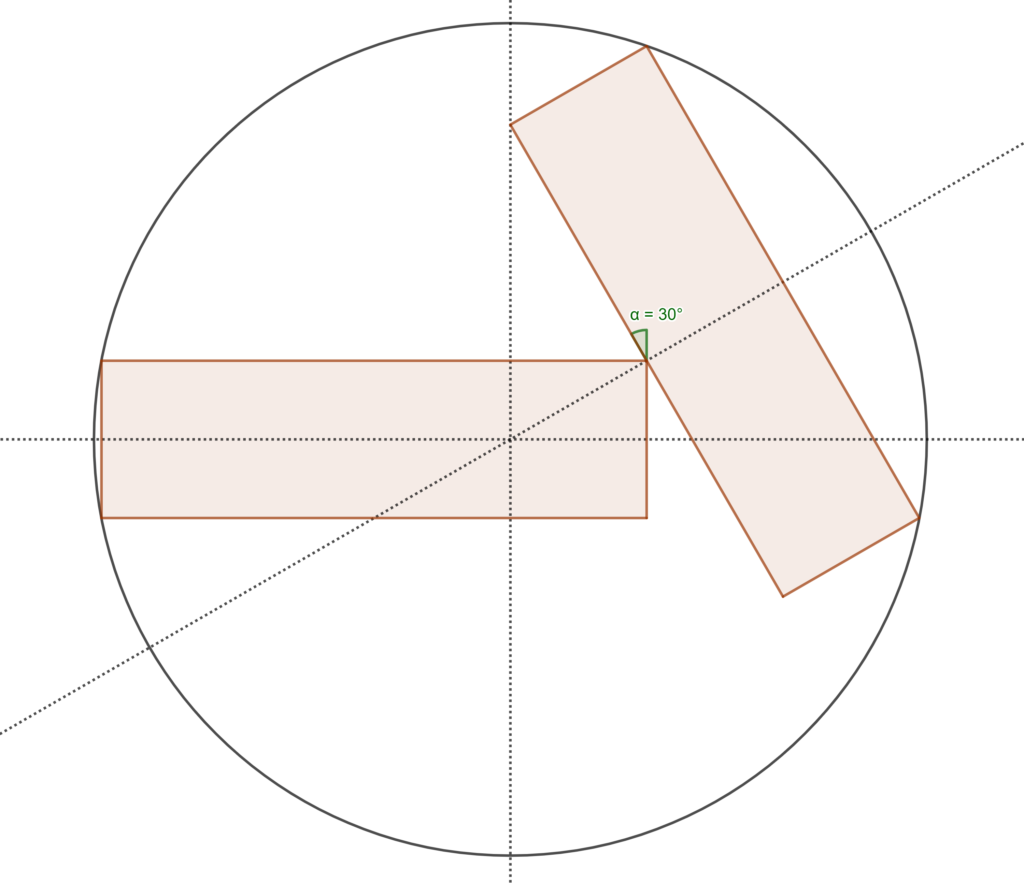
Here is a new geometry problem with two equal rectangles in a circle that you might like to try. The corner of one rectangle touches the midpoint of a side of the other. The left hand rectangle is horizontal in the diagram and the right hand rectangle is tilted 30 degrees from vertical. I created this construction using Geogebra. Ed Staples, who I collaborate with on this series of problems, made the following labelled diagram. Can you find the width 2a of the rectangles in terms of their height h, and the radius of the circle when h is 1?

Following on from my previous puzzle with three equal squares in a semicircle https://convexabacus.xyz/index.php/2022/04/11/three-equal-squares-in-a-semicircle/, here is a more elaborate problem where the three squares are flanked on either side by two half-squares in the shape of isosceles triangles. Assume that the length of the side of the squares is 1, including the orthogonal sides of the two triangles. The four contact points of corners with the circle and the three contact points of corners with the horizontal diameter constrain the construction, defining a unique solution.

I created this diagram in Geogebra, iteratively adjusting it until the corners touch the semicircle, and repeatedly zooming in on one contact point to maximise the accuracy.

I am delighted to report that shortly after posting the diagram on LinkedIn, it was solved by Stéphane Jaubert. His solution is:

radius r = sqrt(30-8.sqrt(10)).

Numerically, this is about 2.16835853. My estimate using Geogebra was off by just -0.000001.

As usual, my online colleague Ed Staples has provided a succinct solution to this problem. I attach his diagram and result below. You can see that he began by bisecting the chord AB and drawing the perpendicular bisector MC. He calculated the radius of the circle as an exact expression involving square roots, which has an approximate numeric value of 1.5213. This is in agreement with the value I found experimentally when using Geogebra to create the problem. The problem statement is here: https://convexabacus.xyz/index.php/2022/04/11/two-unit-squares-in-a-semicircle/

The problem was shared on LinkedIn where it was solved by Mohamad Saleh. He took a different approach using coordinate geometry and simultaneous equations. I attach his work below in two images.

Diagram (above) and solution (below) by Mohamad Saleh.

Two unit squares are jammed inside a semicircle. The left square, whose base lies on the diameter, has a single vertex touching the circle. The right square, tilted 45 degrees such that one diagonal is perpendicular with the diameter has a vertex touching the diameter, a vertex touching the left square and two vertices touching the circle. Can you find an exact expression for the radius of the circle ?

In this construction three unit squares are butted up together inside a semicircle. Each square has a vertex that touches the circumference, and the vertices of two of the squares lie on the diameter shown. The vertical diagonal of the middle square is in line with the circle’s centre, so everything looks quite symmetrical. Can you find the exact value of the radius of the circle? I constructed this arrangement experimentally using Geogebra. I thank Ed Staples for this concise statement of the problem.

This problem was shared on LinkedIn, where it was solved by Stéphane Jaubert who calculated the radius as r=13.sqrt(2)/10. His work is attached below.

In my previous post I presented a geometry problem whimsically called Chopsticks and Bowls. Two circles are contained in rectangle. The distance from the centre of the small circle to the opposite corner of the rectangle is equal to the sum of the diameters of the two circles. The problem is to develop an equation in its simplest form that, when solved, provides the radius of the large circle. The radius of the small circle is given as 1. I am pleased to report that Paul Turner, a retired Mathematics Teacher, has found the solution, shown in the image below.

3+8r-r^2-(4r)(r^.5)=0

Solving this equation is a difficult exercise best suited for a computer algebra system, such as Wolfram Alpha.

The labels in Paul’s solution refer to a diagram by Ed Staples, shown below.

In my previous post Golden Rectangles in a Right Triangle I constructed three golden rectangles in the right-angled triangle with sides of length 3, 4, and 5. I continue this construction by drawing lines through existing points, then marking new points at the intersections of perpendicular lines. This results in two more golden rectangles being identified, these each being flush with one of the perpendicular sides of the triangle and with each other. Their dimensions are 1 x φ and 2 x 2/φ, where φ is the golden ratio. They are shaded in the diagram. A trigonometric proof by Ed Staples shows that φ is indeed key to this construction.

Two mutually tangential circles are contained within a rectangle. The small circle is tangent to two sides of the rectangle, and the large circle is tangent to three of the sides. The distance from the centre of the small circle to the opposite corner of the rectangle is equal to the sum of the diameters of the two circles. Assume that the radius of the small circle is 1. Can you develop an equation in its simplest form that, when solved, provides the exact value of the radius of the large circle? Note that solving this equation is a difficult exercise best suited for a computer algebra system. Note also that the dimensions of the rectangle are a consequence of the construction rather than being a constraint. Thanks are due to Ed Staples who worked with me on this problem, and to Paul Turner who found a succinct solution. You can find their website, with a variety of mathematical puzzles and tutorials, at https://www.mathematicalwhetstones.com/