Geogebra

Geogebra interactive geometry application

A Little Connection between Geometry and Number Theory

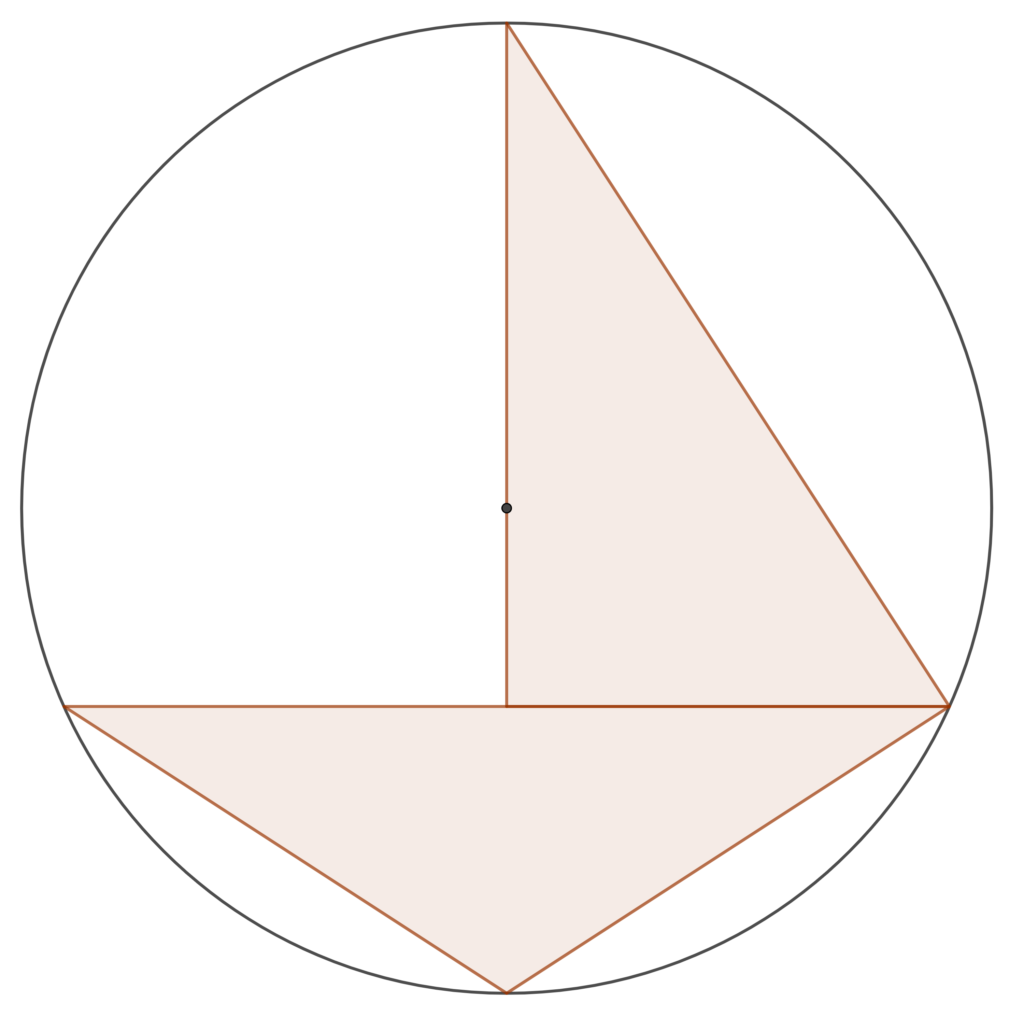
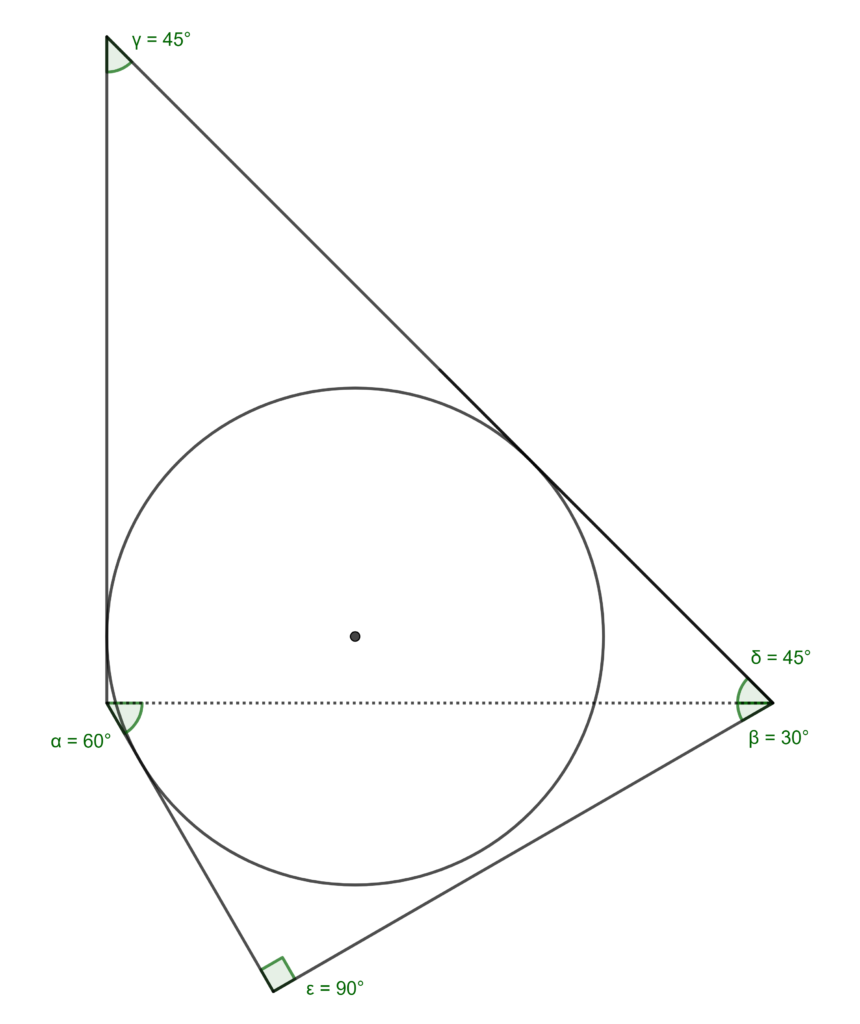
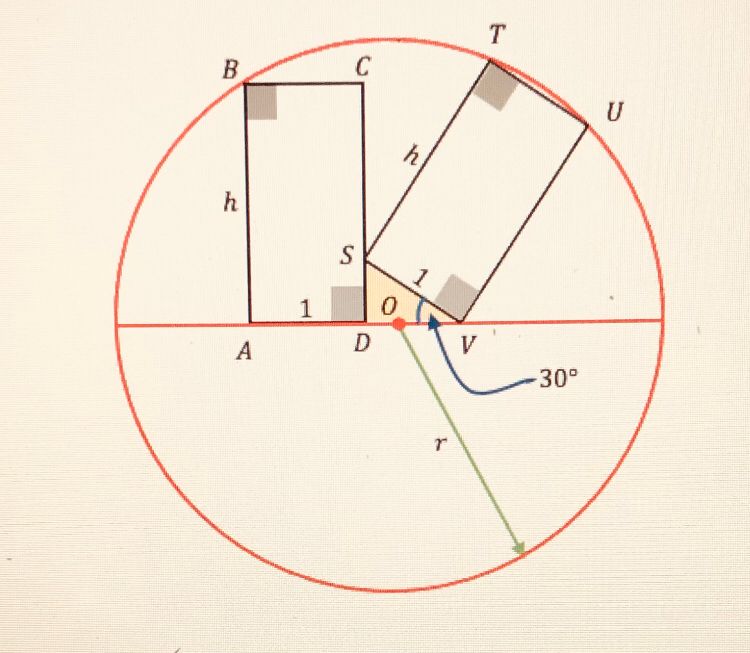
In this geometry problem an isosceles triangle and a right-angled triangle are inscribed in a circle. When you have solved the problem the answer may surprise you, as it has a connection to number theory. The short side of the right-angled triangle has length one and it is coincident with half of the base of the isosceles triangle which has length two. The constraint that defines the problem is that the perimeters of the two triangles are equal. What are the lengths of the other sides and what is the radius of the circle? The diagram shows that the right-angled corner is at the midpoint of the base of the isosceles triangle and that the centre of the circle is a point on the perpendicular side of the right angled triangle.

January 23, 2023 by Geogebra Geometry Mathematics 0

A Rhombus with the Least Possible Perimeter

In this geometry problem circles of radius 1 and radius 2 are tangential and fit in a rhombus such that each circle is tangential to two of its sides. The rhombus has the least possible perimeter. What is the perimeter of the rhombus and the lengths of its diagonals?

January 18, 2023 by Geogebra Geometry 1

A Fourth Problem of Circles in a Quadrilateral

As in the three preceding problems a 30-60-90° triangle is joined to a 45-90-45° triangle, long side to short side to form a composite quadrilateral. Two congruent circles are fitted that are each tangential to two sides of the quadrilateral and are tangential to each other. The diagram is shown with the 45° angle at the top and the right angle at the bottom. The circles are side by side in the diagram and fit precisely. What is the radius of the circles? Scale the diagram as convenient for your calculations.

The first of these four problems was posted here https://convexabacus.xyz/index.php/2023/01/15/a-formula-for-generating-some-geometry-problems/

January 18, 2023 by Geogebra Geometry 0

A Third Problem of Circles in a Quadrilateral

As in the preceeding problems a 30-60-90° triangle is joined to a 45-90-45° triangle, long side to short side to form a composite quadrilateral. Two congruent circles are fitted that are each tangential to two sides of the quadrilateral and are tangential to each other. The diagram is shown with the 45° angle at the top and the right angle at the bottom. The circles are above and below each other in the diagram and fit precisely. What is the radius of the circles? Scale the diagram as convenient for your calculations.

January 18, 2023 by Geogebra Geometry 0

A Second Problem of Circles in a Quadrilateral

As in the first problem a 30-60-90° triangle is joined to a 45-90-45° triangle, long side to short side to form a composite quadrilateral. In this new problem a circle is fitted lower in the diagram such that it is tangential to only the hypotenuse of the 45-90-45° triangle and to two sides of 30-60-90° triangle. What is the radius of the circle? Scale the diagram as convenient for your calculations. Which of these two problems has the bigger circle?

January 18, 2023 by Geogebra Geometry 0

A Formula for Generating some Geometry Problems

I seem to have stumbled on a formula for generating some geometry problems.

(i) Combine two familiar shapes to create a composite irregular polygon.

(ii) Fit one or two circles inside the construction.

(iii) Adjust the shapes to fit precisely.

In this problem a quadrilateral is composed of a 30-60-90° triangle abutting a 45-90-45° triangle, long side to short side. A circle is fitted that is tangential to two sides of the 45-90-45° triangle and to the short side of 30-60-90° triangle. What is the radius of the circle? Scale the diagram as convenient for your calculations. This is the first of a series of four problems.

January 15, 2023 by Geogebra Geometry 1

Two Discs in an Envelope

Two circles are inscribed in a rectangle as shown. One diagonal passes through the point of tangency where the two circles touch, and the other diagonal is tangent to the smaller circle.

You may define the radius of the large circle as 1 and the radius of the small circle as r. Can you find an equation for r, and numeric values for r and for the lengths of the sides of the rectangle?

I created this construction using Geogebra, iteratively adjusting it until everything fitted. The aspect ratio of the rectangle turns out to be about 1.72, a fact that can be used to check your own result. The dimensions of the rectangle are not an initial condition, but a consequence of the radii of the two circles. However, as an alternative exercise try drawing this construction yourself, beginning with a 100 by 172 rectangle.

I am delighted to report that this problem was solved independently by Ted Courant and by Keith Raskin after I posted it on the Math, Math Education, Math Culture group on LinkedIn. They also observed that the rectangle is more accurately drawn with side lengths 1003 and 1725.

May 22, 2022 by Geogebra Geometry Mathematics 1

Isosceles Triangle and Square of Equal Area in a Circle

An isosceles triangle and a square with equal areas are inscribed in a circle as shown. The construction was created using Geogebra, iteratively zooming in and adjusting it until everything fitted precisely. The apex angle of the triangle measures 94.6° approximately, a fact that can be used to check your own analysis. Unable to find algebraic results, I concluded that the exercise for the reader is:

Express simultaneous equations for this construction, and use computer algebra software to find numeric values for the lengths of the edges. You may define the radius of the circle as 1. Note that the base of the triangle is slightly shorter than the diameter of the circle. The centre of the circle is unmarked, locating it being part of the exercise.

An alternative exercise is to take the apex angle as given, define the height of the triangle as 1, and create an accurate construction using trigonometry and a square root calculation.

May 18, 2022 by Computer Algebra Software Geogebra Geometry Trigonometry 0

Two Equal Rectangles in a Semicircle

In this construction two equal rectangles are jammed into a semicircle, one sitting vertically and the other leaning over at a tilt of 30 degrees. The puzzle is described as follows: Two equal rectangles, ABCD and STUV, both have a width 1 but an unknown height h. The left rectangle sits on the diameter of a circle of radius r and has its top left vertex B touching it as shown in the diagram. The right rectangle, leaning at 30 degrees to the diameter, touches the circle at T and U, has its bottom left vertex S touching the left rectangle, and its bottom right vertex V touching the diameter shown. Can you calculate exact expressions for the height h of the rectangles and the radius r of the circle? I thank Ed Staples for this concise statement of my problem, for his diagram shown below, and for his solution which will be shared later. ( Permit a little history. In my first draft the rectangles were of fixed dimension 2 x 1 and the tilt angle was unknown. Unable to solve this, I fixed the tilt angle at 30 degrees and made the height unknown – resulting in nicer problem. )

April 12, 2022 by Geogebra 0

Golden Rectangles in a Right Triangle

This construction was created by experimenting with the Geogebra interactive geometry application. I began with the right-triangle with side lengths 3, 4, and 5. Then I constructed its incircle, which has unit radius. In each of the three corners I inscribed a smaller circle, tangent to the incircle. Considering the circle inscribed in the 3-5 corner, I observed that the numerical value of its radius is 1/φ2, where φ (phi) is the golden ratio, equal to (1+√5)/2. This enables construction of three golden rectangles as shown. The dimensions of the rectangles are 1/φ2 x 1/φ, 1/φ x 1, and 1 x φ.

February 17, 2022 by Geogebra Geometry 2