Colin

A Chopsticks and Bowls Geometric Construction

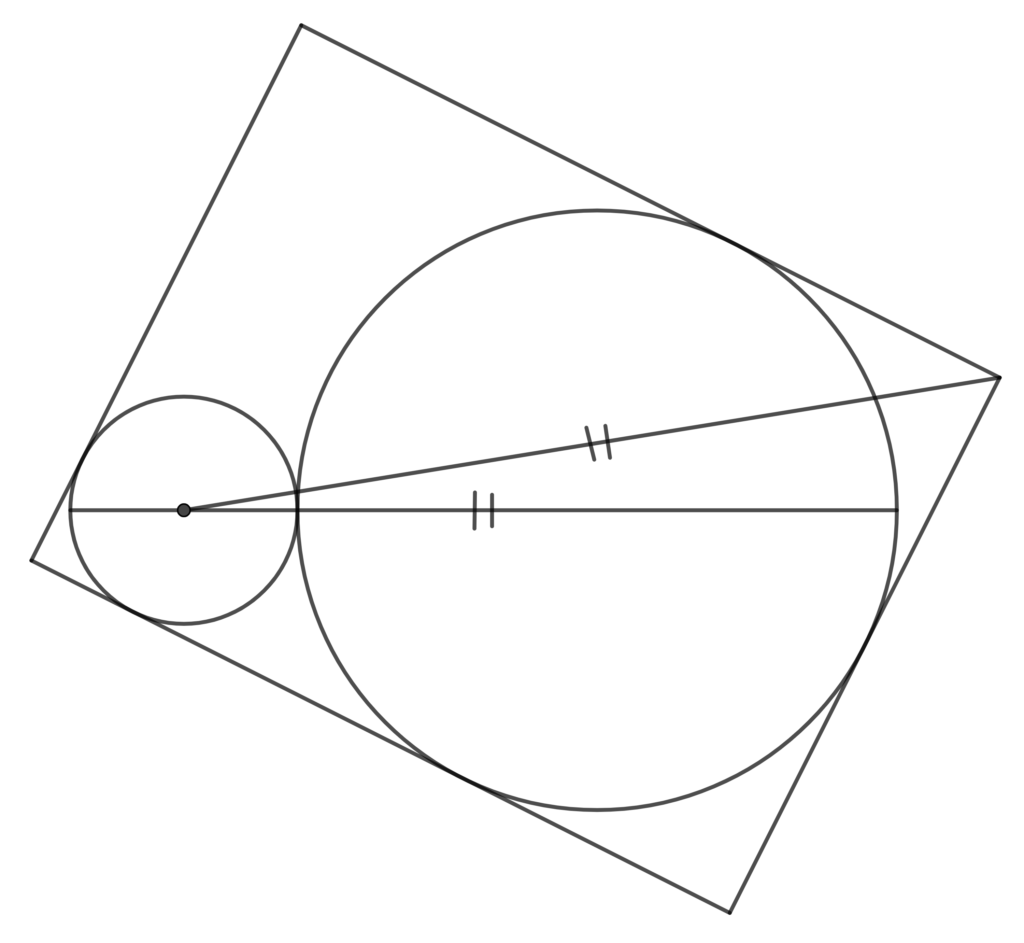
Two mutually tangential circles are contained within a rectangle. The small circle is tangent to two sides of the rectangle, and the large circle is tangent to three of the sides. The distance from the centre of the small circle to the opposite corner of the rectangle is equal to the sum of the diameters of the two circles. Assume that the radius of the small circle is 1. Can you develop an equation in its simplest form that, when solved, provides the exact value of the radius of the large circle? Note that solving this equation is a difficult exercise best suited for a computer algebra system. Note also that the dimensions of the rectangle are a consequence of the construction rather than being a constraint. Thanks are due to Ed Staples who worked with me on this problem, and to Paul Turner who found a succinct solution. You can find their website, with a variety of mathematical puzzles and tutorials, at https://www.mathematicalwhetstones.com/

February 27, 2022 by Geometry 1

Proof that the Golden Ratio is in the 3-4-5 Right Triangle

In my previous post Golden Rectangles in a Right Triangle I inscribed circles in a right-angled triangle with sides of length 3, 4, and 5. I measured that the radius of one inscribed circle was 1/φ2. This was an empirical observation of limited accuracy, not a mathematical proof. Phi or φ, equal to (1+√5)/2, is a transcendental number. Note Paul’s correction in the comments : phi is not transcendental. Fortunately, my colleague Ed Staples was able to prove the length of the radius using trigonometry. His work is shown in the figure. The length r to be calculated is the radius of the small circle inscribed in the corner between the sides of length 3 and length 5. He proves that r = 2 – φ. And, 2 – φ is equal to 1/φ2, which is the value that was determined approximately from the construction. I used the Geogebra software to make this construction. The software conveniently measures lengths and angles, which was particularly useful in this case. You can find Ed Staples’ blog, with a variety of mathematical puzzles and tutorials, at https://www.mathematicalwhetstones.com/blog

February 20, 2022 by Geometry Trigonometry 2

Paper Triangles in a Circle Maximising Area

Three equal right-angled triangles are inscribed in a circle. They are positioned around an equilateral triangle which stabilises the construction. The triangles are cut from paper, with dimensions noted. The right-angled triangles are 7″ x 9” = 17.8 cm x 22.3 cm, and the equilateral triangle has side length 2.46″ = 6.24 cm. The six outermost points are equidistant from the centre of the equilateral triangle, thus lying on a circle, which is not shown. Iterative modelling with Geogebra found that this construction maximises the area of the circle covered by the three right-angled triangles. The ratio 7:9 of side lengths is a rational approximation to a numerical value found experimentally.

February 17, 2022 by Geometry 2

Paper Triangles in a Circle

Three equal right-isosceles triangles are inscribed in a circle. They are positioned around an equilateral triangle which stabilises the construction. The triangles are cut from A4 paper, with dimensions noted. The right triangles have two sides of length 8.3″ = 210 mm, and the equilateral triangle has side length 7.44″ = 188 mm. The six outermost points are equidistant from the centre of the equilateral triangle, thus lying on a circle, which is not shown.

February 17, 2022 by Geometry 2

Golden Rectangles in a Right Triangle

This construction was created by experimenting with the Geogebra interactive geometry application. I began with the right-triangle with side lengths 3, 4, and 5. Then I constructed its incircle, which has unit radius. In each of the three corners I inscribed a smaller circle, tangent to the incircle. Considering the circle inscribed in the 3-5 corner, I observed that the numerical value of its radius is 1/φ2, where φ (phi) is the golden ratio, equal to (1+√5)/2. This enables construction of three golden rectangles as shown. The dimensions of the rectangles are 1/φ2 x 1/φ, 1/φ x 1, and 1 x φ.

February 17, 2022 by Geogebra Geometry 2

An Asymmetric Rolling Shape

This asymmetric rolling shape is based on the 3-4-5 right-triangle. The perimeter is constructed from three arcs of a semicircle, with total length π * r, where r is the common radius of curvature. The shape does not have constant width like the Reuleaux polygons. The construction was created using the Geogebra interactive geometry application. Using a semicircle of fixed radius, the chord lengths in ratio 3:4:5 were found by iterative adjustment.

February 15, 2022 by Geogebra Geometry 0

Introduction

Welcome to my blog about mathematics and technology, with a bit of philosophy. My interests include plane geometry, basic number theory, and computer software. My first posts will explore geometric constructions using computational geometry software. The Fibonacci sequence, algebra, trigonometry and some programming algorithms may be thrown in too.

February 15, 2022 by Uncategorized 2