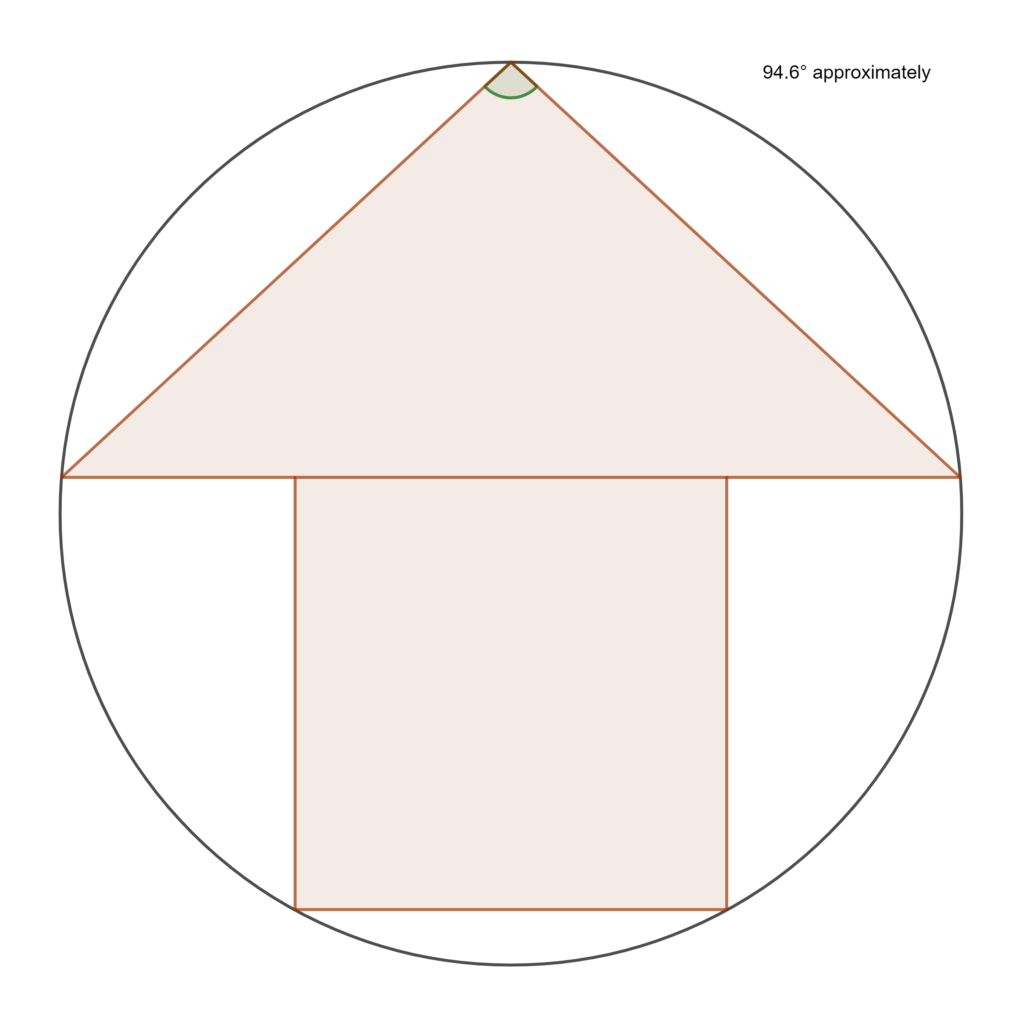
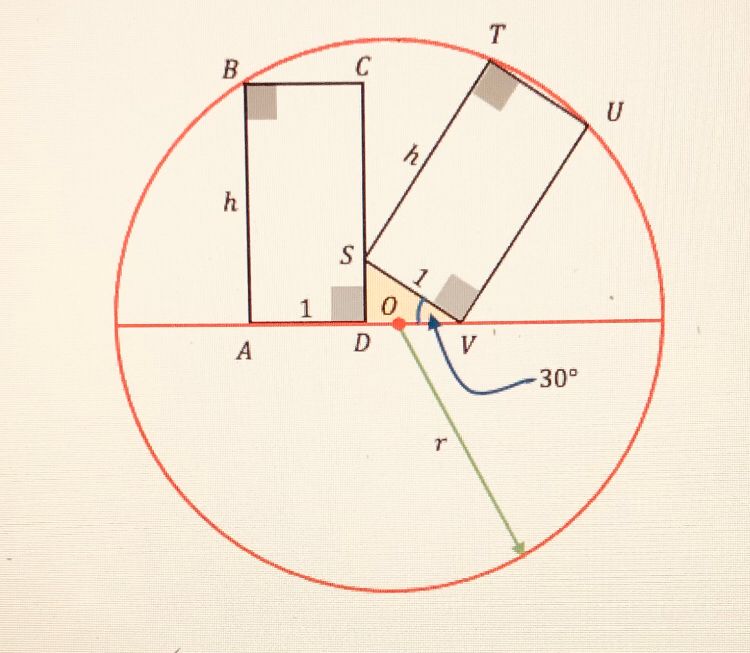
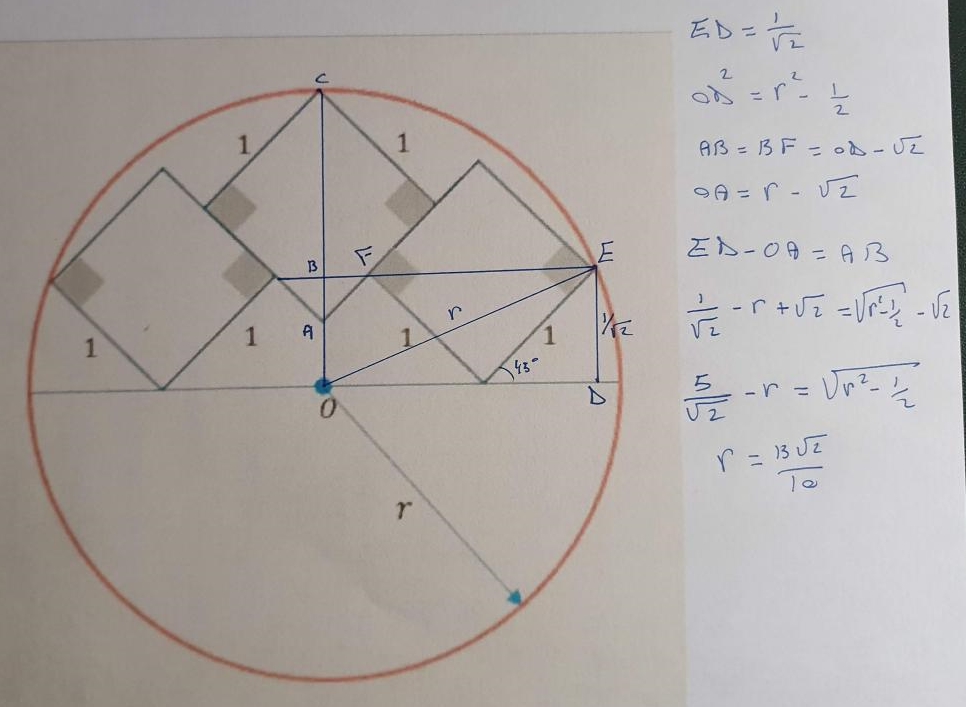
An isosceles triangle and a square with equal areas are inscribed in a circle as shown. The construction was created using Geogebra, iteratively zooming in and adjusting it until everything fitted precisely. The apex angle of the triangle measures 94.6° approximately, a fact that can be used to check your own analysis. Unable to find algebraic results, I concluded that the exercise for the reader is:
Express simultaneous equations for this construction, and use computer algebra software to find numeric values for the lengths of the edges. You may define the radius of the circle as 1. Note that the base of the triangle is slightly shorter than the diameter of the circle. The centre of the circle is unmarked, locating it being part of the exercise.
An alternative exercise is to take the apex angle as given, define the height of the triangle as 1, and create an accurate construction using trigonometry and a square root calculation.