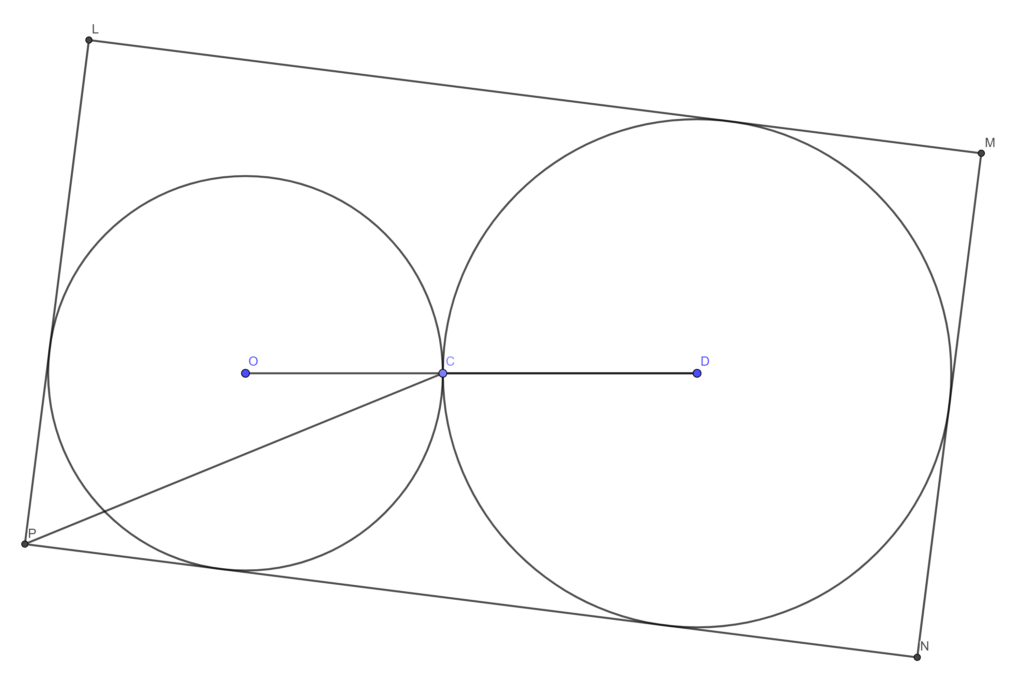
In this geometry problem two circles of different sizes and two line segments of equal length fit precisely in a rectangle. Given that the smaller circle has radius 1, what is the radius r of the larger circle? The circles are mutually tangent at point C as depicted. The unit circle on the left is tangent to two sides of the rectangle, and the larger circle of radius r is tangent to three of the sides. The line segment OD connects the centres of the circles. The rectangle has been adjusted so that the distance from the point of tangency C to the nearest corner P is equal to the length of OD. Can you develop an equation in its simplest form for the radius r? Additionally, express the width and height of the rectangle in terms of r.