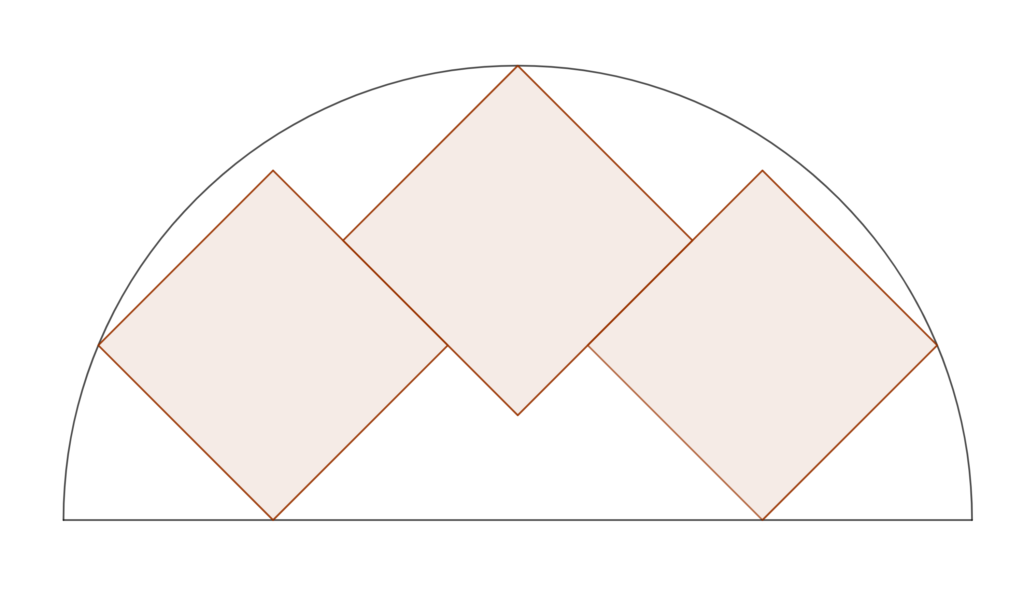
In this construction three unit squares are butted up together inside a semicircle. Each square has a vertex that touches the circumference, and the vertices of two of the squares lie on the diameter shown. The vertical diagonal of the middle square is in line with the circle’s centre, so everything looks quite symmetrical. Can you find the exact value of the radius of the circle? I constructed this arrangement experimentally using Geogebra. I thank Ed Staples for this concise statement of the problem.
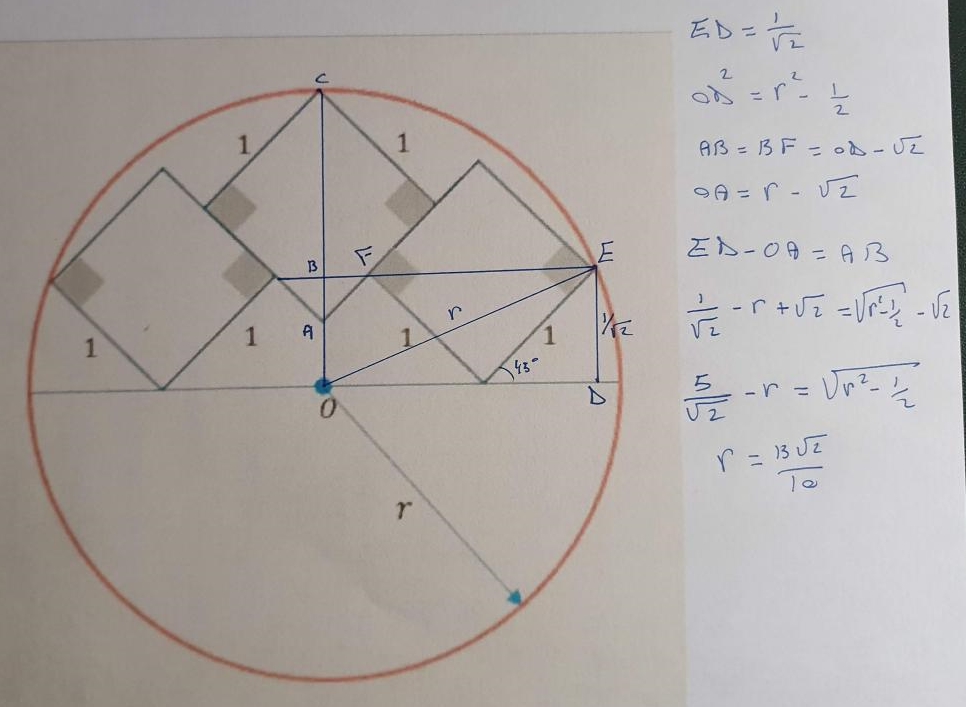
This problem was shared on LinkedIn, where it was solved by Stéphane Jaubert who calculated the radius as r=13.sqrt(2)/10. His work is attached below.