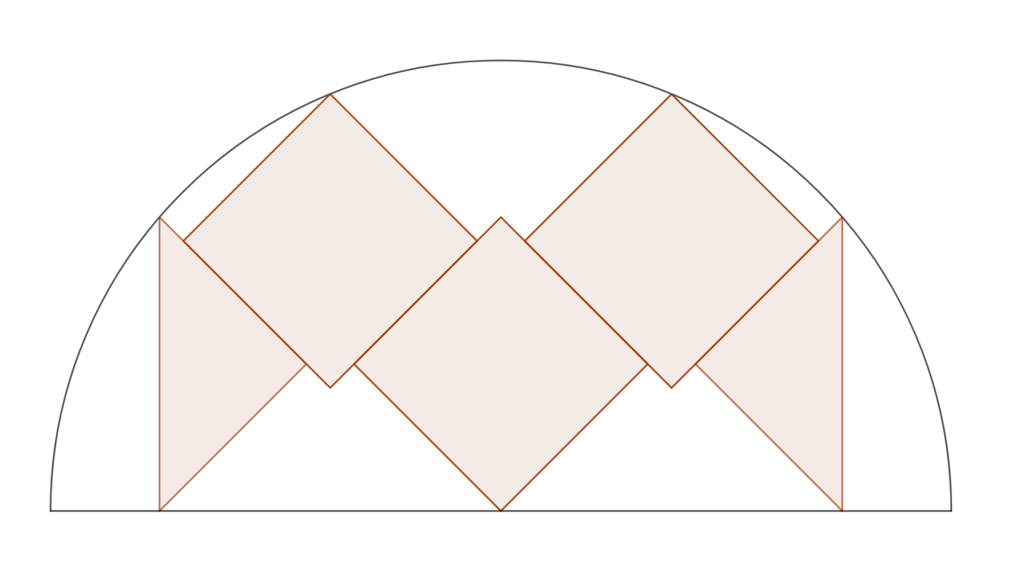
Following on from my previous puzzle with three equal squares in a semicircle https://convexabacus.xyz/index.php/2022/04/11/three-equal-squares-in-a-semicircle/, here is a more elaborate problem where the three squares are flanked on either side by two half-squares in the shape of isosceles triangles. Assume that the length of the side of the squares is 1, including the orthogonal sides of the two triangles. The four contact points of corners with the circle and the three contact points of corners with the horizontal diameter constrain the construction, defining a unique solution.
I created this diagram in Geogebra, iteratively adjusting it until the corners touch the semicircle, and repeatedly zooming in on one contact point to maximise the accuracy.
I am delighted to report that shortly after posting the diagram on LinkedIn, it was solved by Stéphane Jaubert. His solution is:
radius r = sqrt(30-8.sqrt(10)).
Numerically, this is about 2.16835853. My estimate using Geogebra was off by just -0.000001.
