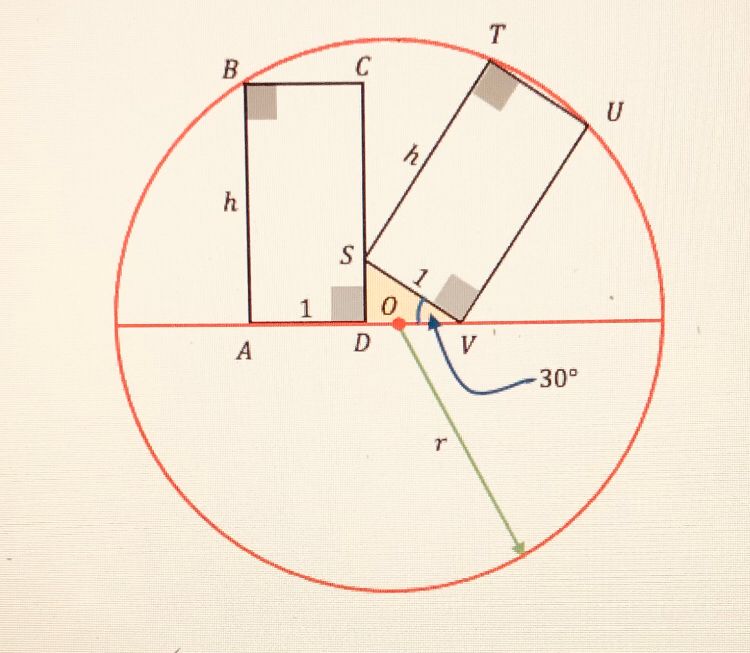
In this construction two equal rectangles are jammed into a semicircle, one sitting vertically and the other leaning over at a tilt of 30 degrees. The puzzle is described as follows: Two equal rectangles, ABCD and STUV, both have a width 1 but an unknown height h. The left rectangle sits on the diameter of a circle of radius r and has its top left vertex B touching it as shown in the diagram. The right rectangle, leaning at 30 degrees to the diameter, touches the circle at T and U, has its bottom left vertex S touching the left rectangle, and its bottom right vertex V touching the diameter shown. Can you calculate exact expressions for the height h of the rectangles and the radius r of the circle? I thank Ed Staples for this concise statement of my problem, for his diagram shown below, and for his solution which will be shared later. ( Permit a little history. In my first draft the rectangles were of fixed dimension 2 x 1 and the tilt angle was unknown. Unable to solve this, I fixed the tilt angle at 30 degrees and made the height unknown – resulting in nicer problem. )